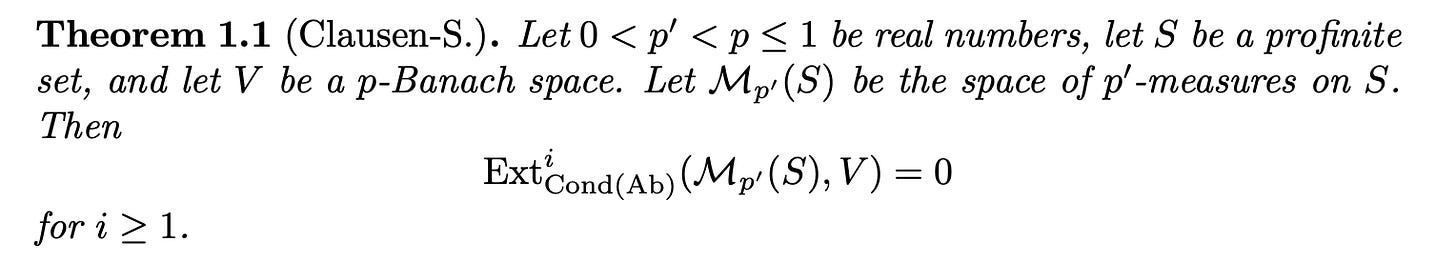Liquid Tensor, language and formalization

Inspired by Clausen-Scholze, I embarked on a gardening adventure.

Peter Scholze once initiated the Liquid Tensor Experiment challenge, details of which you can explore on the Xena Project website: https://xenaproject.wordpress.com/2020/12/05/liquid-tensor-experiment/.

Here’s the theorem.

Oh, I forgot! Peter Scholze wrote something like this (sorry about the formatting, my fault):

The starting point of perfectoid geometry is the idea to study something like a p-adic annulus {T ∈ Cp, |T| = 1} by extracting all p-power roots of T, leading to an infinite tower of covers, and then pass to the limit object, which is a perfectoid space. One wants to do this as, surprisingly, perfectoid spaces are in some ways nicer than the usual annulus; in particular, there is the tilting procedure relating them to characteristic p (and again, surprisingly, characteristic p is in some ways easier than characteristic 0). Technically, one defines the pro-´etale site of the annulus (or any rigid-analytic variety), and shows that locally in the pro-´etale site, the space is perfectoid. But let us forget all about perfectoid geometry, and let us simply look at what the analogue of this story would be for a point

The bold statements underscore the dynamic nature of aggressive representation learning, followed by a shift in direction that facilitates the reuse of concepts. This approach, filled with unexpected discoveries, mirrors the process of creation found in art forms like painting or sculpture, albeit within the constraints of an unforgiving universe.

However, this explanation doesn't fully capture the essence. The real underlying theme is about 'kernels' and a collaborative approach to mathematics that integrates byte-sized contributions, git, semi-formalization, formalization, and natural language to revolutionize the creation of mathematics.

Presently, we're faced with numerous branches, objects, and properties in mathematics, yet we find ourselves unable to 'jump' between them effectively. The concept of 'jumping' shouldn't be the sole strategy. Hence, we're exploring 'higher dimensional jumps' or tactics. To achieve this, enabling human mathematicians is crucial.

Let’s shed some light on what needs to be done.

Identifying Core Properties and Structures: This task has been ongoing, leading to the realization that discoveries in high-dimensional spaces often seem more uncovered than invented. 'Core' implies fundamental aspects that, despite their critical nature, may evolve without widespread notice, altering the foundational blueprint significantly. These properties and structures, akin to meta-objects, can be approximated separately for practical purposes.

As for the properties that are universal across different branches, such as symmetry, invariance, and duality — we need more. Their naming can be standardized and their application can be done using suggest (or similar) in Lean. These properties often hint at deeper connections between seemingly disparate areas, but unfortunately don’t allow efficient (enough) connection building. Here’s how Clausen-Scholze were looking for beautiful gems,

Before giving their definition, let me state a few properties:
– in practice, most topological spaces of interest are “compactly generated weak Hausdorff”. In fact, this is the class of topological spaces customarily used within algebraic topology; also, all usual topological vector spaces (eg., all metrizable ones, or just first-countable ones) have this property. Now compactly generated weak Hausdorff spaces also embed fully faithfully into condensed sets, so in this large class of examples, the transition is completely inconsequential.
– condensed sets have very nice categorical properties, in particular all limits and colimits (like topological spaces). But they also have internal mapping objects: if X, Y are condensed sets, there is a condensed set Hom(X, Y ) such that for any other condensed set T, maps T → Hom(X, Y ) are functorially identified with maps T ×X → Y . In fact, the same is true relatively, for maps over some base condensed set S. In category-speak, “condensed sets are locally cartesian closed”.
– even better, up to mild set-theoretic problems, condensed sets form a topos. (More precisely, they satisfy Giraud’s axioms except for the existence of a set of generators. One can build a variant of the category of condensed sets, known as the category of pyknotic sets of Barwick–Haine, that is a topos,

(again, sorry about the formatting)

Examining existing high-dimensional objects (e.g., tensors, manifolds, complexes) across various branches will help us understand their foundational role. We should consider how these objects encapsulate information, structure, or relationships in their respective domains. Now, doing that with tools and then automating the processes will eventually result in autonomous (albeit not so easily interpretable) math creation. I’ll call it the math world.

The good news is that by understanding how human brain works, the AI creator can provide them with byte-sized lessons. We can learn that a certain type of move in a certain game doesn’t make sense, or that there existing a completely new (surprising) move that we don’t yet understand (and then the AI could explain what concepts it used to get to that information).

The (great) news is that language models captured a bunch of concepts already. And they’ll capture much more.

Abstracting and Generalizing: Could category theory serve as a universal language for mathematics? It's a promising beginning. Viewing category theory not just as a mathematical branch but as a language for abstraction allows for discussions on objects and morphisms that reveal structural similarities across different domains.

Cross-Disciplinary Integration: Bridging concepts from disparate fields such as physics or quantum computing through a common language has proven fruitful, even at a basic level. This interdisciplinary approach is vital for uncovering new mathematical gems.

Innovative Concept Generation: Starting with desired properties or outcomes and working backward to devise mathematical objects or theories showcasing these traits could pave new paths. Computational tools could assist in exploring the realm of potential structures or theories that meet specific criteria.

Iterative Refinement: I also believe in this. I discussed this briefly in Lines and Universes.

I hope you enjoyed it!