On Fixed-Width Rainbows
Ok, this one’s mostly graphs. Cols below are k-prime numbers.
Looks like a rainbow, which reminds me of e (maximizing the product of positive integer widths whose sum, ie. the rainbow width, is fixed).
As we know, for positive integers, the number 3 is particularly efficient in maximizing the product. So let’s re-paint the rainbow.
Introduce the concept of blockers — {3^x+2n+1}.
Then observe:
28 = 3^3 + 2*0 + 1; 3,0
30 = 3^3 + 2*1 + 1; 3,1
84 = 3^4 + 2*1 + 1; 4,1
88 = 3^4 + 2*3 + 1; 4,3
90 = 3^4 + 2*4 + 1; 4,4
100= 3^4 + 2*9 + 1; 4,9
104= 3^4 + 2*11+ 1; 4,11
252= 3^5 + 2*4 + 1; 5,4
264= 3^5 + 2*10+ 1; 5,10
270= 3^5 + 2*13+ 1; 5,13
272= 3^5 + 2*14+ 1; 5,14
280= 3^5 + 2*18+ 1; 5,18
300= 3^5 + 2*28+ 1; 5,28
304= 3^5 + 2*30+ 1; 5,30
312= 3^5 + 2*34+ 1; 5,34
At the same time, observe that, when you start generating such generators (below), there’s quite a bit of 3 in them.
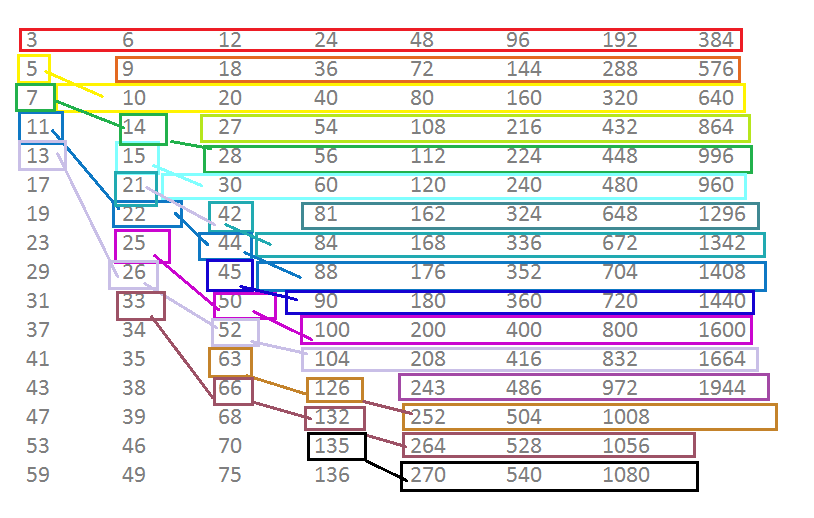
Ok, so let’s finally re-paint the rainbow. Same thing, from a different perspective.
The red sequence is this:
3
9, 10
27, 28, 30
81, 84, 88, 90, 100, 104
243, 252, 264, 270, 272, 280, 300, 304, 312
729, 736, 756, 784, 792, 810, 816, 840, 880, 900, 912, 928, 936, 992, 1000, 1040
2187, 2208, 2268, 2352,2368, 2376,
2430, 2448, 2464, 2520, 2624, 2640,
2700, 2720, 2736, 2752, 2784, 2800,
2808, 2912, 2976, 3000, 3008, 3040, 3120
6561, 6624, 6784, 6804, 7056, 7104, 7128, 7290, 7344, 7360, 7392, \
7552, 7560, 7616, 7744, 7808, 7840, 7872, 7920, 8100, 8160, 8208, \
8256, 8352, 8400, 8424, 8512, 8576, 8736, 8800, 8928, 9000, 9024, \
9088, 9120, 9152, 9280, 9344, 9360
19683, 19840, 19872, 20000, 20224, 20352, 20412, 20608, 20800, 21168, \
21248, 21312, 21384, 21632, 21870, 21952, 22032, 22080, 22176, 22656, \
22680, 22784, 22848, 23232, 23424, 23520, 23616, 23680, 23760, 23936, \
24300, 24480, 24624, 24640, 24768, 24832, 25056, 25200, 25272, 25536, \
25728, 25856, 25984, 26208, 26240, 26368, 26400, 26752, 26784, 27000, \
27072, 27200, 27264, 27360, 27392, 27456, 27520, 27776, 27840, 27904, \
28000, 28032, 28080, 28288, 28928, 29120
Every single col starts with 3^k.
Everything on the right of the red thing, is 2x previous element in the prev col. Or, 1/2 if you divide the other way round.
It feels like multiple perspectives are in play:
integer perspective: the fixed rainbow width,
complex perspective with e: due to the integer perspective, the complex perspective is most likely in play too (we know what’s already in there),
energy perspective: one way looking at language is through energy, and complex numbers allows spinning to obtain energy at a requested frequency. The chart below illustrates the energy perspective.
Instead of approaching that, I had a look at 3. And defined it (well, for now that’s in no way a useful definition; not even a definition) like this:
every interesting number will come through 3,
3 is essentially a combination of 3 transformations: identity, mirror (mirroring the identity), and something that feels like a neutron in an atom.
Happy coding!