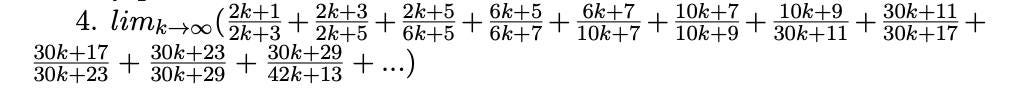Orbit method, automorphic forms, and Gan–Gross–Prasad
Amateur reading "The orbit method and analysis of automorphic forms" by Nelson and Venkatesh.
The magic starts with the development of the quantitative orbit method in microlocal analysis applied to automorphic forms. The method leverages the algebraic group structure to allow for the analysis of (automorphic) forms’ properties. The use case - asymptotic formula for Gan–Gross–Prasad periods across arbitrary ranks. Such formulas can help us capture deep connections in representation theory (I guess, this can be automated as discussed in Lines and Universes).
But before we dig into the use case, let’s briefly talk about branching. Automorphic branching coefficients quantify how automorphic forms decompose when restricted to subgroups. They are significant because they provide insight into the structure of representations of algebraic groups.
The main theorem from the paper states that, under specified conditions, the automorphic branching coefficients exhibit predictable behavior as certain parameters (such as rank) tend to infinity. This reminds me of the Collatz conjecture (even though they seem very unrelated). Here’s why:
Think “manual” deep insights. Both the Collatz conjecture and the theorem on automorphic branching coefficients concern themselves with the predictability of outcomes within infinite or asymptotic processes. In the case of the Collatz conjecture, the interest lies in whether a simple iterative process will inevitably lead to a single outcome (reaching 1) regardless of the starting point. For automorphic branching coefficients, the theorem speculates about the behavior of these coefficients as certain parameters approach infinity. Both cases suggest a deep underlying structure that governs seemingly chaotic or complex systems.
Think completions and high-order structured diagonal arguments. The Collatz conjecture is famous for arising complex and unpredictable behavior from a very simple set of rules. Similarly, the automorphic branching coefficients, while governed by the intricate mathematics of representation theory and automorphic forms, are essentially about understanding how complex behaviors emerge from the fundamental properties and symmetries of algebraic structures as parameters change, particularly in the limit.
Think axioms behind numbers. The Collatz conjecture operates in the realm of discrete mathematics, dealing with integers and sequences. Automorphic branching coefficients, meanwhile, lie at the intersection of continuous mathematics and algebraic structures, particularly in how they relate to the continuous symmetries of Lie groups and the analytic properties of automorphic forms. The conjectured relationship might hint at a deeper, more universal mathematical principle that links discrete behaviors (as in the Collatz conjecture) with the continuous transformations found in the study of automorphic forms and representation theory.
Think scale (and language > communication, and local predictability). Both areas invite exploration into what happens "at the limit" — whether it's the ultimate convergence of a sequence to 1 in the Collatz conjecture or the behavior of branching coefficients as parameters grow without bound. This focus on asymptotic behavior highlights a common mathematical curiosity: understanding the destiny of a process as it extends towards infinity.
Even though the paper is remarkable, the introduction of random matrix theory heuristics made me immediately think of AI. I loved the “manual” part behind the methodology for analyzing automorphic forms (the quantitative orbit method, microlocal analysis, and representation theory). Microlocal calculus (here applied to Lie group representations) is a sophisticated tool for analyzing differential equations and distributions at a very fine scale. Measure classification and equidistribution are also interesting concepts from ergodic theory and measure theory that describe how measures (generalized functions) distribute over spaces.
Now back to branching.
I’ve been running experiments.
Limit based on some fun analysis I used to many years ago
Based on my notes from many years ago -
Some dimensionality reduction code I wrote some time ago
With good enough formalization, language machines could be seen as branching energy. It works for language really well (see market validation). One of the reasons for this is the sheer amount of data (and obviously the genius of the researchers working on those systems).
This time I’ll just ask a question. Will there be enough math papers so that novel math could be auto-generated in 2025 / 2026? Even if the IMO gets solved (or close to solved), will there be novel and inspiring auto-generated math in the coming years (if 2025 is a stretch)?
When could the AI autonomously approach the RH? 3k+1?
I hope you enjoyed it!