Transformer-XL with sliding window, Meliad, DDAR and AlphaGeometry
Been playing around with Lean, and got inspired by the PFR formalization. Love the topic of formalization / theorem proving / mathematical and general purpose reasoning.
The formalization of the PFR proof was a fascinating undertaking. I’ve been playing with Lean for a while, and it really inspired me to experiment further. But doing formalization directly is quite hard (see the code below from Mathematics in Lean)
variable {𝕜 : Type*} [NontriviallyNormedField 𝕜] {E : Type*} [NormedAddCommGroup E]
[NormedSpace 𝕜 E] {F : Type*} [NormedAddCommGroup F] [NormedSpace 𝕜 F]
open Metric
example {ι : Type*} [CompleteSpace E] {g : ι → E →L[𝕜] F} (h : ∀ x, ∃ C, ∀ i, ‖g i x‖ ≤ C) :
∃ C', ∀ i, ‖g i‖ ≤ C' := by
-- sequence of subsets consisting of those `x : E` with norms `‖g i x‖` bounded by `n`
let e : ℕ → Set E := fun n ↦ ⋂ i : ι, { x : E | ‖g i x‖ ≤ n }
-- each of these sets is closed
have hc : ∀ n : ℕ, IsClosed (e n) := fun i ↦
isClosed_iInter fun i ↦ isClosed_le (g i).cont.norm continuous_const
-- the union is the entire space; this is where we use `h`
have hU : (⋃ n : ℕ, e n) = univ := by
refine' eq_univ_of_forall fun x ↦ _
rcases h x with ⟨C, hC⟩
obtain ⟨m, hm⟩ := exists_nat_ge C
exact ⟨e m, mem_range_self m, mem_iInter.mpr fun i ↦ le_trans (hC i) hm⟩
/- apply the Baire category theorem to conclude that for some `m : ℕ`,
`e m` contains some `x` -/
obtain ⟨m : ℕ, x : E, hx : x ∈ interior (e m)⟩ := nonempty_interior_of_iUnion_of_closed hc hU
obtain ⟨ε, ε_pos, hε : ball x ε ⊆ interior (e m)⟩ := isOpen_iff.mp isOpen_interior x hx
obtain ⟨k : 𝕜, hk : 1 < ‖k‖⟩ := NormedField.exists_one_lt_norm 𝕜
-- show all elements in the ball have norm bounded by `m` after applying any `g i`
have real_norm_le : ∀ z ∈ ball x ε, ∀ (i : ι), ‖g i z‖ ≤ m := by
intro z hz i
replace hz := mem_iInter.mp (interior_iInter_subset _ (hε hz)) i
apply interior_subset hz
have εk_pos : 0 < ε / ‖k‖ := div_pos ε_pos (zero_lt_one.trans hk)
refine' ⟨(m + m : ℕ) / (ε / ‖k‖), fun i ↦ ContinuousLinearMap.op_norm_le_of_shell ε_pos _ hk _⟩
· exact div_nonneg (Nat.cast_nonneg _) εk_pos.le
intro y le_y y_lt
calc
‖g i y‖ = ‖g i (y + x) - g i x‖ := by rw [(g i).map_add, add_sub_cancel]
_ ≤ ‖g i (y + x)‖ + ‖g i x‖ := (norm_sub_le _ _)
_ ≤ m + m :=
(add_le_add (real_norm_le (y + x) (by rwa [add_comm, add_mem_ball_iff_norm]) i)
(real_norm_le x (mem_ball_self ε_pos) i))
_ = (m + m : ℕ) := by norm_cast
_ ≤ (m + m : ℕ) * (‖y‖ / (ε / ‖k‖)) :=
(le_mul_of_one_le_right (Nat.cast_nonneg _)
((one_le_div <| div_pos ε_pos (zero_lt_one.trans hk)).2 le_y))
_ = (m + m : ℕ) / (ε / ‖k‖) * ‖y‖ := (mul_comm_div _ _ _).symm
end
So how to we get to (even more) intelligent machines? Think value chain and value capture. Tech builders had to go for conviction, determination, traction, teams and technology. Mathematicians spoke a different language. Programmers, too. But many of the tech builders actually love math and programming. The same applies to mathematicians who want to do machine learning, or programmers who want to build durable solutions. We need to unite, not divide. And work together. Even in the mathematics world, we have many different styles.
Mathematicians have done mathematics differently throughout centuries. Ramanujan and Hardy were very different, and had completely different backgrounds. The age (Wiles) and the background (Huh) are becoming less relevant. Conviction and resilience will prevail. The renaissance of mathematics is coming.
Doing formalization directly could be to some extent sped up by LLMs (written proof → Lean proof), but it will still take enormous work that will need to be done by mathematicians. At the same time, working on ML already requires (at least at the moment) significant math and programming skills.
Direct formalization, however, won’t be fast enough. There’s more than one process leading to what we’ll see in the future. Here’re some of them:
natural language to formalization in math,
natural language to program verification,
developer co-pilots,
experiments with traction and potential (see AlphaGeometry from Google DeepMind),
models for programming tasks (Code Llama from Meta) and program synthesis (CodeGen from Salesforce),
Blueprint-like next-gen creator tools
(there’s more)
But let’s forget about this for a moment.
I was re-reading "Transformer-XL: Attentive Language Models.Beyond a Fixed-Length Context", Zihang Dai, Zhilin Yang, Yiming Yang,Jaime Carbonell, Quoc V. Le, Ruslan Salakhutdinov ("enables learning dependency beyond a fixed length without disrupting temporal coherence") and then check out Transformer-XL with sliding window ("segment length is limited only by available device memory", "the cache is not differentiable, whereas the sliding window is, so there is some benefit to using segments that are longer than the window length"), Memorizing Transformer("memory and the T-XL cache work well together; the memory is used for long-range lookups, while the cache is used for short-range lookups") and Block-Recurrent Transformer("Recurrence serves a similar role to external memory, but is faster.") in Meliad.
I was also thinking about a conversation with a friend of mine (a mathematician) whom I once showed a conjecture, and then we spent hours thinking what can be done about it. It turns out that proving there’s a connection (a potentially very interesting one!) between two somewhat disconnected topics is really hard. It takes determination to pursue such problems. Exploration of the problem space and connecting the otherwise “disconnected” is hard.
And then I thought about AlphaGeometry from Google DeepMind. And whether we could start learning physics from videos (and sports streaming)?
Meliad is great for research. You get to tweak stuff and experiment. But if you think about value chains and value capture (even in the context of advancing math) , AlphaGeometry (together with jax, flax and t5) used it to do something quite magical. You need the library and the models, and the simplicity, and the ability to experiment. But that’s never enough. One needed lots of conviction and energy to make it work.
So I got even more excited about AlphaGeometry (I love Lean too, but it’s very different if you could get a (semi-)formalization out of an LLM), and wanted to share my thoughts.
AlphaGeometry appeared in Nature - https://www.nature.com/articles/s41586-023-06747-5 “Solving olympiad geometry without human demonstrations”, Trieu H. Trinh, Yuhuai Wu, Quoc V. Le, He He & Thang Luong
The repository is part of DeepMind's project on AlphaGeometry, a system designed to solve IMO-level geometry problems. That’s an example from the repo:
graph.py:468] translated_imo_2000_p1
graph.py:469] a b = segment a b; g1 = on_tline g1 a a b; g2 = on_tline g2 b b a; m = on_circle m g1 a, on_circle m g2 b; n = on_circle n g1 a, on_circle n g2 b; c = on_pline c m a b, on_circle c g1 a; d = on_pline d m a b, on_circle d g2 b; e = on_line e a c, on_line e b d; p = on_line p a n, on_line p c d; q = on_line q b n, on_line q c d ? cong e p e q
ddar.py:41] Depth 1/1000 time = 1.7772269248962402
ddar.py:41] Depth 2/1000 time = 5.63526177406311
ddar.py:41] Depth 3/1000 time = 6.883412837982178
ddar.py:41] Depth 4/1000 time = 10.275688409805298
ddar.py:41] Depth 5/1000 time = 12.048273086547852
alphageometry.py:190]
==========================
* From theorem premises:
A B G1 G2 M N C D E P Q : Points
AG_1 ⟂ AB [00]
BA ⟂ G_2B [01]
G_2M = G_2B [02]
G_1M = G_1A [03]
...
[log omitted]
...
036. ∠QEB = ∠(QP-EA) [46] & ∠(BE-QP) = ∠AEP [55] ⇒ ∠EQP = ∠QPE [56]
037. ∠PQE = ∠EPQ [56] ⇒ EP = EQ
==========================How does it work?
There’re two modes in it:
DDAR (Deductive and Algebraic Reasoning)
Alphageometry (with the model, beam size etc.)
if _MODE.value == 'ddar':
g, _ = gh.Graph.build_problem(this_problem, DEFINITIONS)
run_ddar(g, this_problem, _OUT_FILE.value)
elif _MODE.value == 'alphageometry':
model = get_lm(_CKPT_PATH.value, _VOCAB_PATH.value)
run_alphageometry(
model,
this_problem,
_SEARCH_DEPTH.value,
_BEAM_SIZE.value,
_OUT_FILE.value,
)
The math concepts first. Here’s a couple of examples (not all of them):
Nodes is the base class of all geometric entities. Points, circles, lines can be nodes.
Lots of utility functions that can be used by other projects, too.
get_lines_thru_all, get_circles_thru_all: Retrieve lines or circles passing through given points.
line_of_and_why, circle_of_and_why: Determine the line or circle that passes through given points and explain why (using dependencies).
all_angles, all_ratios: Generate all angles or ratios for given directions or lengths.
cross: Generates all possible pairs (Cartesian product) of elements from two lists.
comb2, comb3, comb4: Generate all combinations of 2, 3, and 4 elements, respectively, from a given list.
perm2, perm3, perm4: Generate all permutations of 2, 3, and 4 elements, respectively, from a given list.
all_4points, all_8points: Generate all combinations of 4 or 8 points from given lines. These are likely used to explore geometric configurations involving points on these lines.
Functions like solve_quad, line_line_intersection, line_circle_intersection, etc., provide utilities for calculating intersections and solving geometric problems.
There are numerous functions for checking geometric conditions (check_coll, check_para, etc.) and for sketching or constructing geometric entities (sketch_line, sketch_circle, etc.).
Drawing and visualization: Functions for drawing geometric figures using matplotlib, such as draw_point, draw_line, draw_circle, and more.
Tables for geometric computation: Classes like Table, GeometricTable, RatioTable, AngleTable, and DistanceTable are designed to store and manipulate algebraic representations of geometric entities and their relationships.
Complex geometric operations: Functions within these classes perform operations like adding equality expressions (add_expr), managing equivalent entities (update_groups), and computing relationships (add_eq, add_const_ratio, add_eqratio, etc.). Reminds us of formalization?
Generators for combinations and permutations: Functions like comb2, perm2, and chain2 are used to generate combinations and permutations of elements, which are essential in exploring geometrical relationships and properties.
Traceback for algebraic reasoning: Functions such as why in the Table class provide a mechanism to trace back the reasoning or steps taken to arrive at a particular geometric conclusion.
Flax/Beam-related:
One script inspired by a beam search example from the Flax library, which is a neural network library for JAX (a numerical computation library by Google).
Beam search: The script includes features like continued decoding from a previous beam cache and initialization with a single beam that can expand into multiple beams (efficiency!) Also, flattening and unflattening beams and beam_search_flat function (seed token, cache, tokens to logits, masking etc.)
Support for brevity penalty: The brevity_penalty function suggests that the beam search implementation includes a mechanism to penalize shorter sequences.
Custom data structures: The BeamState class is a data structure to store the state of the beam search process.
Efficient computation with JAX: The script uses JAX operations (jax.tree_util.tree_map, lax.top_k, lax.while_loop) for efficient computation and to handle the parallel nature of beam search.
The system:
Graph-based geometric representation: The graph-based approach to representing geometric objects and their relationships.
Deductive reasoning: Deductive reasoning over geometric configurations. It uses rules (theorems) to deduce new geometric facts from existing ones.
Complex rule matching: The script can handle various complex geometrical rules and theorems, as shown by the extensive list of match_ functions.
BFS-based strategy: Exploration of the space of geometric constructions systematically. The representation of geometric constructions and proofs as a graph, where nodes represent geometric entities and edges represent relationships or properties.
Algebraic and geometric integration:
By associating geometric objects with algebraic entities (like Measure, Length, Direction), the script integrates geometric reasoning with algebraic calculations.
Ranking:
The script includes a ranking system (RANKING) for different types of geometric entities, likely used for ordering or prioritization in problem-solving algorithms.
Utility methods like is_equiv, is_equal, and bfs_backtrack provide functionality for checking equivalences and tracing back through the graph structure.
A couple of interesting functions:
saturate_or_goal function:
This function aims to run the Deductive Database (DD) method until either no further facts can be deduced (saturation) or a specific goal is achieved.
It takes a graph representation of a geometric problem (gh.Graph), a list of geometric theorems (pr.Theorem), and a problem instance (pr.Problem) as inputs.
The function iteratively applies the DD method, which involves breadth-first search (BFS) through the space of possible geometric deductions, to extend the graph with new facts.
The process stops upon reaching a maximum level (max_level), finding the goal, or when no new facts are deduced, indicating saturation.
solve function:
This function alternates between using DD and Algebraic Reasoning (AR) to solve a geometric problem until the specified goal is found or the search space is exhausted.
It handles the overall process, including managing time constraints (timeout) and the depth of the search (max_level).
The function returns the final state of the geometric graph, the time taken at each level, the solution status (e.g., 'solved' or 'saturated'), branching information, and all deductions made.
get_proof_steps function:
This function extracts the sequence of proof steps that led to the solution or the final state of the geometric graph.
It uses the trace_back module to backtrack and construct the proof sequence.
The function returns structured information about the proof, including setup steps, auxiliary constructions, and the main proof steps.
Language model:
Wrapper around Meliad for language model (LM) inference.
The constructor (__init__) takes parameters for the vocabulary path, directory to load the model from, and an inference mode (defaulting to 'beam_search').
It sets up a SentencePieceVocabulary, which is commonly used for tokenizing text in language models.
It initializes a Trainer object with various configurations, including dataset iterators and the directory to load the model from. The model is initialized and configured for inference with specific settings related to the neural network's architecture (like the number of heads and head size in a transformer model).
They execute the model inference using JAX operations, handling batching and state management. It returns various outputs, including sequences, scores, and the updated state.
What then attracted my attention was how problems and theorems have been handled:
Construction: Represents a geometric predicate or a basic geometric statement.
Clause: Represents a set of constructions. It's a more complex geometric statement that can consist of multiple constructions.
Problem: Encapsulates a geometric problem, consisting of multiple clauses and potentially a goal or conclusion.
Definition: Defines the construction statements, which are basic building blocks for defining geometric entities and their relationships.
Theorem: Represents a deduction rule, consisting of premises and a conclusion.
Then everything becomes a DAG. And the DAG:
point_levels: Reformats a setup (collection of dependencies) into levels based on point constructions.
point_log: Groups point constructions in the setup into a log format.
setup_to_levels: Transforms the setup into levels of point constructions.
separate_dependency_difference: Identifies and separates different types of dependencies related to a query (or problem).
recursive_traceback: Recursively traces back from a query (conclusion) to identify the sequence of dependencies leading up to it.
So it’s A LOT about dependencies. And graphs. It made me re-read “EXPHORMER: Sparse Transformers for Graphs”, Hamed Shirzad, Ameya Velingker, Balaji Venkatachalam, Danica J. Sutherland, Ali Kemal Sinop.
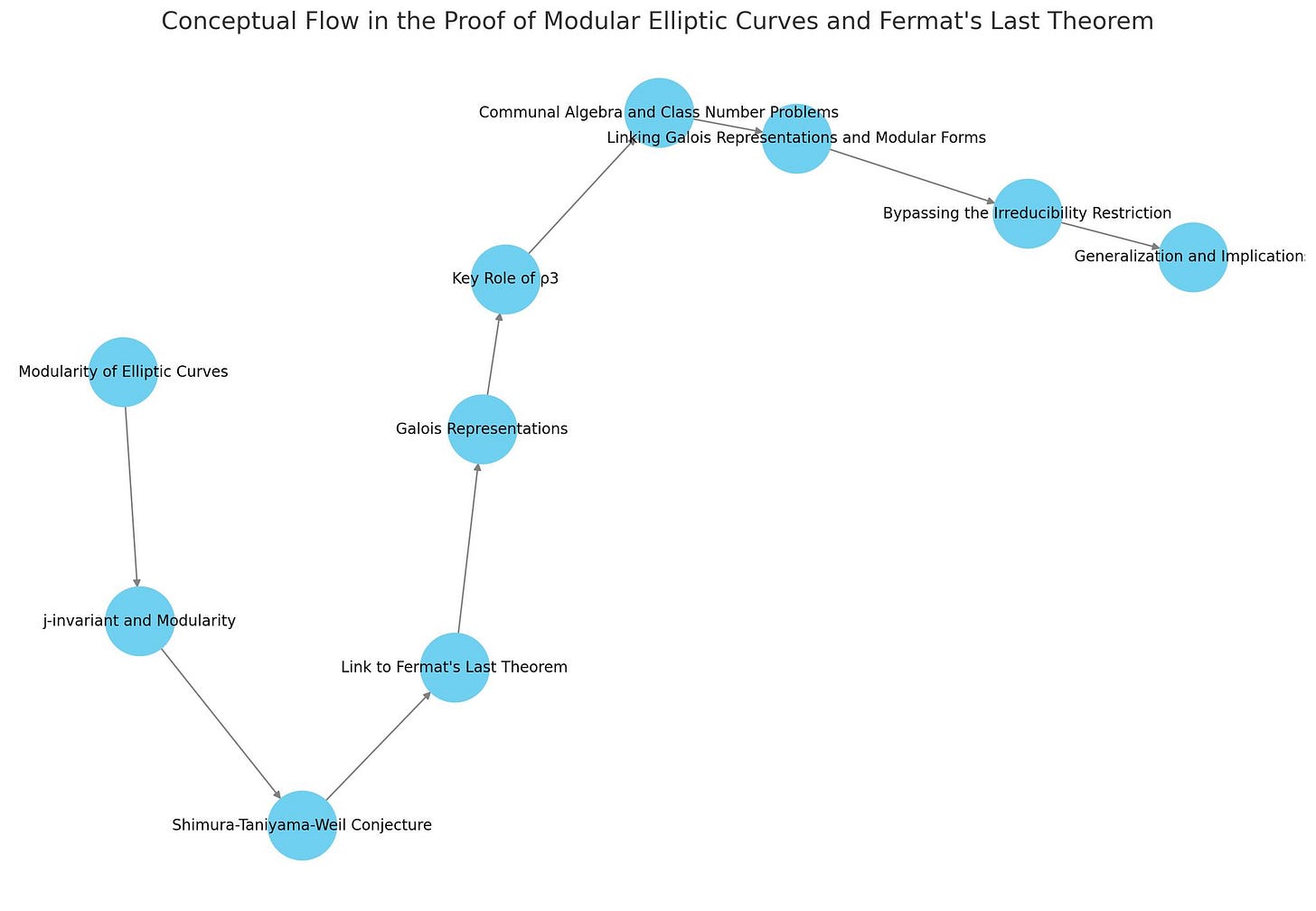
One can also get overviews of solutions from LLMs, but they are not perfect / still extremely useful (I did it some time ago for the FLT).
As for the proofs. The solution is first initialized as a string and formatted in sections. Then, the solution string is appended with a header for theorem premises.For each set of premises and associated points in the setup data structure, the points are formatted and added to the solution string. If there are no premises for a given set of points, it continues to the next iteration. Each premise is converted to natural language using the natural_language_statement function and appended to the premises_nl list with a reference number.
(there’s also the Auxiliary Constructions Section:
Similar to the theorem premises section, this part deals with auxiliary constructions used in the proof.
It follows a similar pattern of listing points and their corresponding premises in natural language.)
Then there’s some known deduction rules. A dictionary r2name maps rule names (like 'r32', 'r33') to their natural language equivalents (like '(SSS)', '(SAS)'). That gives us more readable, human-friendly representation of the proof steps.
Finally, the proof steps. The solution string is appended with a header for proof steps. The proof steps are iterated over, and each step is converted to a natural language string using the proof_step_string function. The rule_name of each step is replaced with its corresponding natural language representation from the r2name dictionary. Each proof step is formatted with a step number and appended to the solution string.
DDAR gets the following arguments:
g: An object of type gh.Graph, representing the current state of the proof. This graph likely holds nodes and edges representing geometric entities and their relationships.
p: An object of type pr.Problem, which contains the problem statement that needs to be solved.
out_file: A string specifying the path to the output file where the solution, if found, will be written.
It runs the DD+AR algorithm. The function starts by calling ddar.solve, passing the graph g, a set of rules (RULES), the problem p, and a maximum level limit (max_level=1000). This is presumably the core logic where DD+AR attempts to find a solution to the problem. After the DD+AR algorithm runs, the function checks if the solution is found. This is done by converting the goal's arguments (p.goal.args) into nodes in the graph (g.names2nodes) and then checking if these satisfy the goal (g.check). If the goal is not achieved, it logs a failure message and returns False. If the goal is successfully achieved, the solution is written to the specified output file using the write_solution function. The function then calls gh.nm.draw with various geometric entities like points, lines, circles, and segments from the graph.
RunAlphageometry mode, on the other hand, is designed to run a proof search algorithm, named AlphaGeometry, on a given geometric problem. This algorithm likely combines natural language processing (via a language model) with geometric reasoning. It takes the following arguments:
model: An instance of lm.LanguageModelInference, which is likely an interface for interacting with a language model that can process and infer geometric problems.
p: An object of type pr.Problem, which contains the geometric problem statement to be solved.
search_depth: An integer specifying the maximum depth for the proof search. Deeper searches might explore more complex proof paths.
beam_size: An integer that sets the beam size for the search algorithm. A larger beam size allows the algorithm to explore more potential proof paths simultaneously.
out_file: A string specifying the path to the output file where the solution, if found, will be written.
The proof search algorithm implements the core structure of the AlphaGeometry proof search and involves many optimizations and abstractions, particularly those dependent on specific infrastructures like multi-GPU setups or parallel execution, are removed to simplify the presentation of the core algorithm. It returns a boolean value indicating whether the problem was successfully solved. If a solution is found, it's written to the specified output file (out_file).
Now, back to Lean.. (to be continued) I hope you liked it.